本文分为 理论介绍 和 Python 代码示例 两部分
理论介绍
线性回归模型
单变量线性回归
$$ h_ {\theta } (x)= \theta _ {0} + \theta _ {1} x $$
|
|
代价函数
为了评估出线性函数拟合的怎么样,需要使用到 Cost Function(代价函数),代价函数越接近 0,说明越好,等于 0 的时候即为完全拟合。
$$ J( \theta _ {0} , \theta _ {1} )= \frac {1}{2m} \sum _ {i=1}^ {m} (h_ {\theta }(x^ {(i)})-y^ {(i)})^2 $$
|
|
梯度下降
梯度的本意是一个向量(矢量),表示某一函数(该函数一般是二元及以上的)在该点处的方向导数沿着该方向取得最大值,即函数在该点处沿着该方向(此梯度的方向)变化最快,变化率最大(为该梯度的模)。
当函数是一元函数时,梯度就是导数。这里我们用一个最简单的例子来讲解梯度下降法,然后推广理解更为复杂的函数。
还是用上面的例子,有 n 组数据,自变量 $x(x1,x2,…,xn)$ ,因变量 $y(y1,y2,…,yn)$ ,但这次我们假设它们之间的关系是:$f(x)=ax$ 。记 $J(a)$ 为 $f(x)$ 和 $y$ 之间的差异,即:
$$ J(a)= \sum _ {i=1}^ {n} (f( x^ {(i)} - y^ {(i))^ {2}} = \sum _ {i=1}^ {n} (ax^ {(i)}-y^ {(i)})^ {2} $$在梯度下降法中,需要我们先给参数 a 赋一个预设值,然后再一点一点的修改 a,直到 J(a) 取最小值时,确定 a 的值。下面直接给出梯度下降法的公式(其中 $\alpha$ 为正数):
$$ repeat\{ a:=a- \alpha \frac {\partial J(a)}{\partial a} \} $$
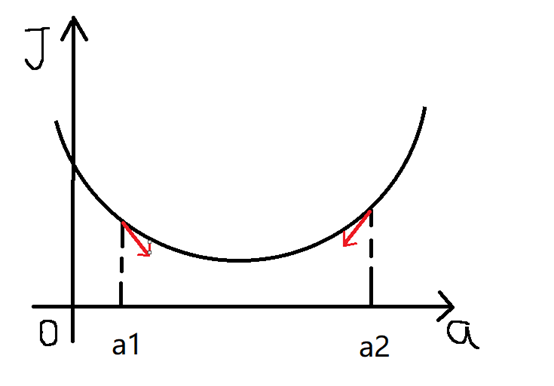
如果给 $a$ 去的预设值是 $a1$ ,那么 $a$ 对 $J(a)$ 的导数为负数,意味着 $a$ 会向右移。然后重复这个步骤,直到 $J(a)$ 到达最小值。
同理给 $a$ 取得预设值是 $a2$ ,那么 $a$ 对 $J(a)$ 的导数为正数,意味着 $a$ 会向左移,然后重复这个步骤,直到 $J(a)$ 到达最小值。
因此我们可以得到,不管 $a$ 的预设值取多少, $J(a)$ 经过梯度下降法的多次重复后,最后总能到达最小值。
对于上述公式的理解可以用上山下山的例子来说明,给 a 的预设值就好比是你正处在一个山的山坡上,如果你想走到山谷,那么你就会判断你是向左还是向右走,走完第一次之后又会重新判断。在公式中 $\alpha$ 叫做学习率,也就是你走的步伐的大小, $\alpha$ 越大,步伐就越大,当然, $\alpha$ 也不是越大越好,就好比如果你就快到山谷了,但是由于步伐太大而刚好跨过山谷,下一步往回走又会跨过山谷,这样就永远到不了山谷了。
|
|
多变量线性回归
多变量线性回归于单变量线性回归其实差不了多少,只是需要计算的参数从两个变成多个了而已。
假设有 n 组数据,其中目标值(因变量)与特征值(自变量)之间的关系为:
$$ f(x(i))= \theta _ {0} + \theta _ {1} x_ {1}^ {(i)} + \cdots + \theta _ {n} x_ {n}^ {(i)} $$其中 $i$ 表示第 $i$ 组数据,损失函数为:
$$ J( \theta )= \sum _ {i=1}^ {n} (f( x^ {(i)} - y^ {(i)})^ {2} $$梯度下降法公式为:
$$ repeat \{\theta _ {j} := \theta _ {j} - \alpha \frac {\partial J(\theta )}{\partial \theta _ {j}}\} $$Python 代码示例
|
|