本文分为 理论介绍 和 Python 代码实现 两部分

👉 点此直接跳转到代码实现

什么是逻辑回归

当看到“回归”这两个字时，可能会误以为逻辑回归是一种解决回归问题的算法。然而，逻辑回归实际上是一种通过回归的思想来解决二分类问题的算法。

逻辑回归如何解决分类问题

逻辑回归通过将样本特征与样本所属类别的概率联系起来。假设已经训练好一个逻辑回归模型为 $f(x)$，则模型的输出表示样本 $x$ 的标签为 1 的概率，即

根据此概率，可以推断：当 $\hat{p} > 0.5$ 时，$x$ 属于标签 1；否则，属于标签 0。因此，可以表示为：

其中，$\hat{y}$ 是样本 $x$ 根据模型预测出的标签结果。标签 0 和标签 1 的具体含义可以根据实际业务需求来决定，例如在癌细胞识别中，0 代表良性肿瘤，1 代表恶性肿瘤。

由于概率是 0 到 1 的实数值，逻辑回归可以看作是一种回归算法，如果仅计算样本所属标签的概率；如果需要对样本进行分类，则逻辑回归是一种二分类算法。

逻辑回归中的概率计算

逻辑回归的概率计算与线性回归相关。在线性回归中，通过训练一组参数 $W^T$ 和 $b$ 来拟合样本数据，线性回归的输出为：

但此时 $\hat{y}$ 的值域为 $(-\infty, +\infty)$，如果能将值域从 $(-\infty, +\infty)$ 转换为 $(0, 1)$ 的概率值，就可以解决分类问题。为此，逻辑回归将线性回归的输出作为输入，传递给另一个可以将实数转换为概率值的函数——Sigmoid 函数。则转换后的概率为：

这里的 $\sigma$ 就是 Sigmoid 函数。

Sigmoid 函数

Sigmoid 函数的公式为：

其图像如下：

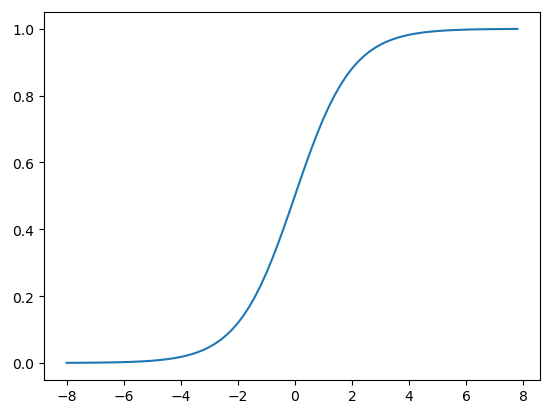
从 Sigmoid 函数的图像可以看出，当 $t$ 趋近于 $-\infty$ 时，函数值趋近于 0；当 $t$ 趋近于 $+\infty$ 时，函数值趋近于 1。因此，Sigmoid 函数的值域是 $(0, 1)$，符合我们将 $(-\infty, +\infty)$ 的实数转换为 $(0, 1)$ 概率值的需求。

因此，逻辑回归在预测时可以表示为：

Python 代码实现

1
2
3
4
5
6
7
8

import numpy as np

def sigmoid(t):
    '''
    :param t: 负无穷到正无穷的实数
    :return: 转换后的概率值
    '''
    return 1 / (1 + np.exp(-t))