本文分为 理论介绍 和 Python 代码实现 两部分
👉 点此直接跳转到代码实现
Logistic 回归
Logistic 回归属于机器学习中的监督学习,它是一种利用回归的思想来解决分类问题的经典二分类分类器。由于其训练后的参数具有较强的可解释性,Logistic 回归通常被用作基线模型(baseline model),便于后期更好地挖掘业务相关信息或提升模型性能。
逻辑回归的特点
优点:
缺点:
适用数据类型:数值型和标称型数据。
Sigmoid 函数
我们需要的函数应该能够接受所有的输入并预测出类别。在二分类情况下,该函数的输出应为 0 或 1。可能你之前接触过具有这种性质的函数,例如海维赛德阶跃函数(Heaviside step function),也被称为单位阶跃函数。然而,海维赛德阶跃函数的问题在于其在跳跃点上从 0 瞬间跳跃到 1,这种瞬间跳跃过程有时较难处理。
幸运的是,Sigmoid 函数具有类似的性质,并且在数学上更容易处理。Sigmoid 函数的具体公式如下:
$$ \sigma(x) = \frac{1}{1 + e^{-x}} $$下图展示了 Sigmoid 函数在不同坐标尺度下的两条曲线。当 $x=0$ 时,Sigmoid 函数值为 0.5;随着 $x$ 的增大,Sigmoid 函数值逼近于 1;而随着 $x$ 的减小,Sigmoid 函数值逼近于 0。如果横坐标刻度足够大,Sigmoid 函数看起来很像一个阶跃函数。
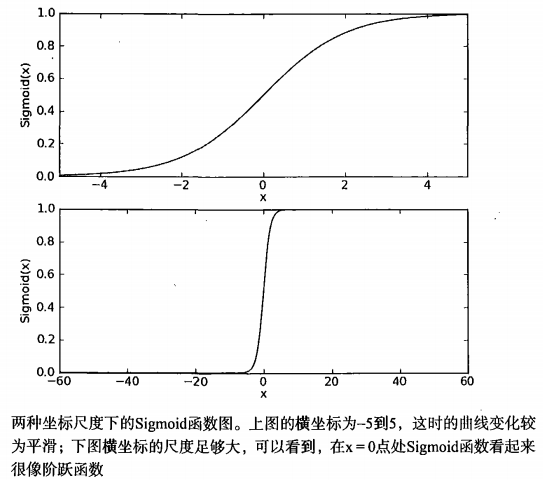
因此,为了实现 Sigmoid 回归分类器,我们可以在每个特征上乘以一个回归系数,并将所有结果值相加。然后将这个总和代入 Sigmoid 函数中,得到一个范围在 0 到 1 之间的数值。任何大于 0.5 的数据被分类为 1 类,任何小于 0.5 的数据则被归为 0 类。这样,Logistic 回归也可以被看作一种概率估计方法。
Python 代码实现
使用前请注意修改 loadDataSet() 函数中的文件名
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
|
import numpy as np
'''
Parameters:
无
Returns:
dataMat - 数据列表
labelMat - 标签列表
'''
# 函数说明:加载数据
def loadDataSet():
dataMat = [] #创建数据列表
labelMat = [] #创建标签列表
fr = open('testSet.txt') #打开文件
for line in fr.readlines(): #逐行读取
lineArr = line.strip().split() #去回车,放入列表
dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])]) #添加数据
labelMat.append(int(lineArr[2])) #添加标签
fr.close() #关闭文件
return dataMat, labelMat #返回
'''
Parameters:
inX - 数据
Returns:
sigmoid 函数
'''
# 函数说明:sigmoid 函数
def sigmoid(inX):
return 1.0 / (1 + np.exp(-inX))
'''
Parameters:
dataMatIn - 数据集
classLabels - 数据标签
Returns:
weights - 权重数组
'''
# 函数说明:梯度上升算法
def gradAscent(dataMatIn, classLabels):
dataMatrix = np.mat(dataMatIn) #转换成 numpy 的 mat
labelMat = np.mat(classLabels).transpose() #转换成 numpy 的 mat,并进行转置
m, n = np.shape(dataMatrix) #返回 dataMatrix 的大小。m 为行数,n 为列数。
alpha = 0.001 #移动步长,也就是学习速率,控制更新的幅度。
maxCycles = 500 #最大迭代次数
weights = np.ones((n,1)) #初始化权重
for k in range(maxCycles): #进行迭代
h = sigmoid(dataMatrix * weights) #计算预测出的概率值
error = labelMat - h #计算错误
weights = weights + alpha * dataMatrix.transpose() * error #更新权重
return weights.getA() #将矩阵转换为数组,返回权重数组
if __name__ == '__main__':
dataMat, labelMat = loadDataSet()
print(gradAscent(dataMat, labelMat))
|
