机器学习 - 损失函数

本文分为 理论介绍 和 Python 代码实现 两部分

理论

损失函数概述

机器学习中的监督学习本质上是给定一系列训练样本 $(x_{i},y_{i})$ ，尝试学习 $x$ 与 $y$ 间的映射关系。损失函数（Loss Function）则是这个过程中关键的一个组成部分，用来衡量模型的输出 $\hat{y}$ 与真实的 $y$ 之间的差距，给模型的优化指明方向。

平均绝对误差损失

平均绝对误差损失（Mean Absolute Error Loss）是一种常见的损失函数，也称 L1损失。

$$ J_{M A E}=\frac{1}{N} \sum_{i=1}^{N}\left|y_{i}-\hat{y}_{i}\right| $$

其可视化图像如图所示

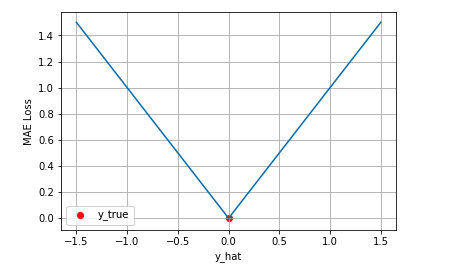
平均绝对误差损失函数图像

从图中可以看出 MAE 损失的最小值为 0（当预测等于真实值时），最大值为无穷大。随着预测与真实值绝对误差 $∣y− \hat{y}∣$ 的增加，MAE 损失呈线性增长。

均方差损失

均方差损失（Mean Squared Rrror Loss）也是一种在机器学习以及深度学习回归任务中常用的一种损失函数，也成为L2损失。

$$ J_{M S E}=\frac{1}{N} \sum_{i=1}^{N}\left(y_{i}-\hat{y}_{i}\right)^{2} $$

下面是是对于真实值 $y=0$ ，不同的预测值 [−1.5,1.5]的均方差损失的变化图

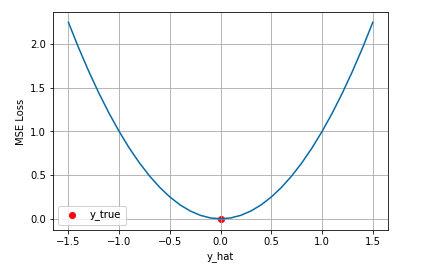
均方差损失函数图像

从图可以看到随着预测值与真实值绝对误差 $∣y− \hat{y}∣$ 的增加，均方差呈二次方增增加。

交叉熵损失

前面介绍的两种损失函数都是适用于回归问题的，对于分类问题，常用的损失函数是交叉熵损失函数（Cross-entropy Loss）。

二分类

在进行二分类时，我们通常使用 Sigmoid 函数将模型的输出压缩到 (0,1) 区间内 $\hat{y}_{i} \in (0,1)$ ，用来代表给定输入 $x_i$ ，模型判断为正类的概率。由于只有正负两类，因此同时也得到了负类的概率。

$$ p( y_ {i} = 1|x_ {i} )= \widehat {y}_ {i} p( y_ {i} = 0|x_ {i} )=1- \widehat {y}_ {i} $$

将其合并后可得

$$ p(y_i|x_i) = (\hat{y_i})^{y_i} (1-\hat{y_i})^{1-y_i} $$

假设数据点之间独立同分布，则似然可以表示为

$$ L(x, y)=\prod_{i=1}^N(\hat{y_i})^{y_i} (1-\hat{y_i})^{1-y_i} $$

对似然取对数，然后加负号变成最小化负对数似然，即为交叉熵损失函数的形式

$$ J_{CE}=-\sum_{i=1}^N\left (y_i{log(}\hat{y_i}) + (1- y_i){log}(1-\hat{y_i})\right) $$

其可视化图像如图

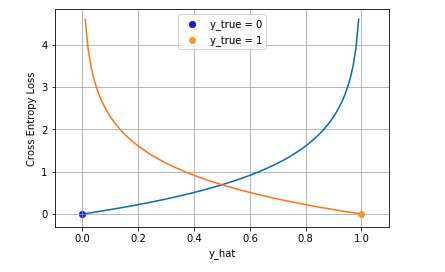
二分类交叉熵损失函数图像

其中蓝线是目标值为 0 时输出不同输出的损失，黄线是目标值为 1 时的损失。可以看到越接近目标值损失越小，随着误差变大，损失呈指数增长。

多分类

在多分类的任务中，交叉熵损失函数的推导思路和二分类是一样的，变化的地方是真实值 $y_i$ 现在是一个 One-hot 向量，同时模型输出的压缩由原来的 Sigmoid 函数换成 Softmax 函数。Softmax 函数将每个维度的输出范围都限定在 (0, 1) 之间，同时所有维度的输出和为 1，用于表示一个概率分布。

$$ p(y_i|x_i) = \prod_{k=1}^K(\hat{y_i}^k)^{y_i^k} $$

其中 $k \in K$ 表示 $K$ 个类别中的一类，同样的假设数据点之间独立同分布，可得到负对数似然为

$$ J_{CE} = -\sum_{i=1}^N\sum_{k=1}^K y_i^k \mathbb{log}(\hat{y_i}^k) $$

由于 $y_i$ 是一个 one-hot 向量，除了目标类为 1 之外其他类别上的输出都为 0，因此上式也可以写为

$$ J_{CE} = -\sum_{i=1}^N y_i^{c_i}\mathbb{log}(\hat{y_i}^{c_i}) $$

其中 $c_i$ 是样本 $x_i$ 的目标类。通常这个应用于多分类的交叉熵损失函数也被称为 Softmax Loss 或者 Categorical Cross Entropy Loss。

Python 代码实现

平均绝对误差损失

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13


def mean_absolute_loss(self,y_hat,y,n):
	"""
    平均绝对误差损失
    :param y_hat: 预测结果
    :param y: 真实结果
    :param n: 样本数量
    :return: 损失函数计算结果
    """
    
    loss = abs(y_hat - y)
    loss = np.sum(loss) / n
    
    return loss

均方差损失

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13


def mean_squared_loss(self,y_hat,y,n):
    """
    均方差损失
    :param y_hat: 预测结果
    :param y: 真实结果
    :param n: 样本数量
    :return: 损失函数计算结果
    """
    
    loss = (y_hat - y) ** 2
    loss = np.sum(loss) / n
    
    return loss

交叉熵损失

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14


def cross_entropy_loss(self,y_hat,y,n):
    """
    交叉熵损失
    :param y_hat: 预测结果
    :param y: 真实结果
    :param n: 样本个数
    :return: 损失函数计算结果
    """

    loss = y_hat * np.log2(y) + (1 - y) * np.log2(1 - y)
    loss = np.sum(loss)
    loss = loss / (-n)
    
    return loss