本文分为 理论介绍 和 Python 代码实现 两部分
Softmax 回归原理
与逻辑回归一样,Softmax 回归也是一个分类算法,不过它用于多分类问题。我们的数据有多少个特征,就有多少个输入;有多少个类别,就有多少个输出。
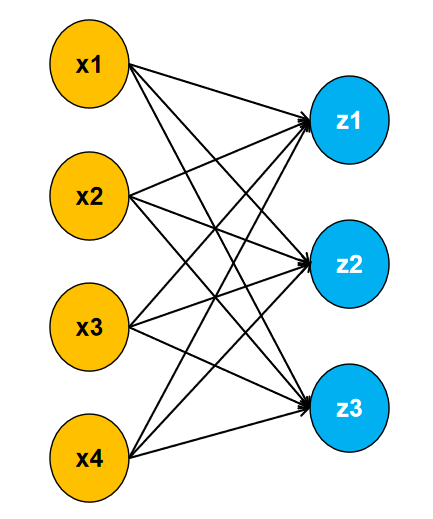
如图所示,假设我们的数据有四个特征和三个类别。每个输入与输出之间都有一个权重相连接,且每个输出都有一个对应的偏置。具体公式如下:
$$ z_1 = x_1 w_{11} + x_2 w_{12} + x_3 w_{13} + x_4 w_{14} + b_1 $$$$ z_2 = x_1 w_{21} + x_2 w_{22} + x_3 w_{23} + x_4 w_{24} + b_2 $$$$ z_3 = x_1 w_{31} + x_2 w_{32} + x_3 w_{33} + x_4 w_{34} + b_3 $$输出 $z_1$, $z_2$, $z_3$ 的值大小,代表了样本属于每个类别的可能性。比如,若 $z_1 = 1$, $z_2 = 10$, $z_3 = 100$,则表示该样本更有可能属于类别 $z_3$。
然而,直接将这些输出作为样本属于某个类别的可能性存在一些问题。举个例子,若你得到一个输出为 10,你可能觉得样本属于该类别的可能性很大,但若另外两个输出分别为 1000 和 2000,这时候该样本实际上不太可能属于输出为 10 的类别。因此,我们需要将输出统一到一个合理的范围内,比如 0 到 1 之间。这样,如果某个输出的值为 0.9,我们就可以非常确定它属于该类别。
Softmax 函数
Softmax 函数的公式如下:
$$ \hat y_ {i} = \frac {exp((z_ {i}))}{\sum _ {i=1}^ {l-1}exp(z_ {i})} $$其中,$i$ 表示第 $i$ 个类别,$c$ 为总类别数。由公式可知:
$$ 0 \leq \hat{y}_i \leq 1 $$且
$$ \sum_{i=1}^{c} \hat{y}_i = 1 $$这样就可以将输出的值转换到 0 到 1 之间,并且总和为 1。每个类别对应的输出值可以被视为样本属于该类别的概率。
对于单个样本,假设一共有 0, 1, 2 三个类别,输出对应为 $[0.2, 0.3, 0.5]$,则最终判断该样本属于类别 2。
Python 代码实现
|
|